5.1.3 Representación De Relaciones
(Matrices, Conjunto, Grafos,
Diagrama de flechas)
Representación De
Relaciones Usando Matrices
Un método para el estudio de las
relaciones de manera algorítmica es utilizando matrices compuestas de ceros y
unos.
Sean A y B conjuntos finitos de
la forma:
Si R es una relación de A en B. La relación
R puede ser representada por la matriz 
donde:
donde:
La matriz 
se denomina matriz de R. En otras palabras
la matriz, de ceros y unos, de R tiene un 1 en la posición 
cuando 
está relacionado con 
y un 1 en está posición
si
no está relacionado con 
.
se denomina matriz de R. En otras palabras
la matriz, de ceros y unos, de R tiene un 1 en la posición cuando está relacionado con y un 1 en está posiciónsi .
Obsérvese en la definición anterior que
los elementos de A y B han sido escritos en
un orden particular pero arbitrario. Por lo tanto, la matriz que representa una
relación.
depende de los órdenes usados para A y B.
Cuando A = B usamos el mismo orden para A y B.
EJEMPLO:
Sean 
Consideremos la siguiente relación de
:
Entonces la matriz de R es
Recíprocamente, dando los
conjuntos A y B con m y n elementos respectivamente,
una matriz de m x n formada
de ceros y unos determina una relación de A en B.
Representación De
Relaciones Usando Conjuntos
Un conjunto es una colección de objetos
considerada como un objeto en sí. Los objetos de la colección pueden ser
cualquier cosa: personas, números, colores, letras, figuras, etc. Cada uno de
los objetos en la colección es un elemento o miembro del
conjunto. Por ejemplo, el conjunto de los colores del arcoíris es:
AI = {Rojo, Naranja,
Amarillo, Verde, Azul, Añil, Violeta}
Un conjunto suele definirse mediante una propiedad que todos sus
elementos comparten. Por ejemplo, para los números naturales, si consideramos
la propiedad de ser un número primo, el conjunto de los número primos es:
P = {2, 3, 5, 7,
11, 13, …}
Un conjunto queda definido únicamente por sus miembros y por nada
más. En particular el orden en el que se representen estos es irrelevante.
Además, cada elemento puede aparecer de manera idéntica una sola vez, esto es,
no puede haber elementos totalmente
idénticos repetidos. Por ejemplo:
S = {Lunes, Martes,
Miércoles, Jueves, Viernes} = {Martes, Viernes, Jueves, Lunes, Miércoles}
AI = {Rojo, Naranja,
Amarillo, Verde, Azul, Añil, Violeta} = {Rojo, Naranja, Amarillo, Verde, Azul,
Añil, Violeta, Naranja}
Los conjuntos pueden ser finitos o infinitos. El conjunto de
los número naturales es infinito, pero el conjunto de los planetas en el
sistema solar es finito (tiene ocho elementos). Además, con los conjuntos
pueden combinarse mediante operaciones, de manera similar a las operaciones con
números.
Los conjuntos son un concepto básico, en el sentido de que no
es posible definir los en términos de nociones más elementales, por
lo que su estudio puede realizarse de manera informal, apelando a la intuición
y a la lógica. Por otro lado, son el concepto fundamental de la matemática:
mediante ellos puede formularse el resto de objetos matemáticos, como los
números y las funciones, entre otros. Su estudio detallado requiere pues la
introducción de axiomas y conduce a la teoría de conjunto.
Representación De
Relaciones Usando Grafos
Informalmente, un grafo es un conjunto de objetos llamados
vértices o nodos unidos por enlaces llamados aristas o arcos,
que permiten representar relaciones binaria entre elementos de un conjunto.
Típicamente, un grafo se representa gráficamente como un conjunto
de puntos (vértices o nodos) unidos por líneas (aristas).
Un grafo G es
un par ordenado G = (V,E), donde:
· V es un conjunto de vértices o nodos, y
· E es un conjunto de aristas o arcos, que
relacionan estos nodos.
Normalmente V suele
ser finito. Muchos resultados importantes sobre grafos no son aplicables
para grafos infinitos.
Se llama orden del grafo G a su número de
vértices, | V | .
El grado de un vértice o nodo V es igual al número de arcos E que se encuentran en él.
Un bucle es una arista que relaciona al mismo nodo; es decir,
una arista donde el nodo inicial y el nodo final coinciden.
EJEMPLO:
· V:={1,2,3,4,5,6}
· E:={{1,2},{1,5},{2,3},{2,5},{3,4},{4,5},{4,6}}
El hecho que el vértice 1 sea adyacente con el vértice 2 puede ser
denotado como 1 ~ 2.
En las teorías de las categorías una categoría puede
ser considerada como un multígrafo dirigido, con los objetos
como vértices y los morfismos como aristas dirigidas.
Representación De
Relaciones Usando Diagramas De Flechas
Una forma de representar el producto cartesiano es el diagrama de flechas.
Una forma de representar el producto cartesiano es el diagrama de flechas.
Escriba los elementos de a y los elementos de b en dos
discos disyuntos, y luego dibuje una flecha de ” a e a “ en ” b e
b” cada vez que a este relacionado con b.
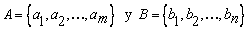
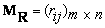
gracias, me sirvió de mucho
ResponderEliminargracias
ResponderEliminargracias
ResponderEliminar